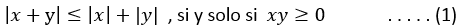Distancia entre dos puntos

Para determinar la distancia entre dos puntos A y B vamos primero a deducir la fórmula general para ese fin y después la podremos aplicar en cualquier situación que se nos presente, es decir que los puntos cuya distancia queramos determinar puedan encontrarse en cualquiera de los cuatro cuadrantes del plano cartesiano.

Si tenemos dos punto A y B que forman el segmento a, como se ve en la  siguiente figura:

Las coordenadas de los puntos A y B se muestran en la siguiente figura:

Tracemos ahora una línea paralela al eje X  que pase por el punto A y que se corte en el punto M con otra paralela al eje Y que pase por B.

La distancia entre los puntos A y M es simplemente la diferencia entre sus abscisas, así como la distancia entre los puntos B y M es la diferencia entre sus ordenadas.

Considerando el teorema de Pitágoras, se cumple que:

Es decir que el valor absoluto del segmento a es igual a la distancia entre los puntos A y B e igual a la raíz cuadrada de la suma de los cuadrados de la diferencia entre abscisas y la diferencia entre ordenadas de los mismos puntos

Desigualdad Triangular

¿Qué es la desigualdad triangular?

Se trata de una propiedad de los números reales, que nos dice que el valor absoluto de la suma de dos números es menor o igual a la suma de los valores absolutos de cada uno, siempre que ambos sean positivos o ambos negativos.

O escrito en lenguaje matemático:

Aplicación:

Si se desea determinar en qué caso la siguiente expresión es cierta:

Si hacemos que:

Tendríamos:

Y como podemos apreciar es de la misma forma que la expresión (1), por lo que podemos decir que la expresión (2) es válida siempre que:

Es decir:

   

Serie1.Puntos y Rectas.Ejercicio 2

Demuestra que el triángulo cuyos vértices son los puntos A(1,1), B(2,3), C(5,-1) es un triángulo rectángulo.

Solución:

De acuerdo a la figura y según el teorema de Pitágoras, si

entonces el triángulo de la figura será rectángulo.

 

Se puede ver entonces que  

por lo que el triángulo formado por los puntos ABC es rectángulo, LQ.Q.D.

Serie1.Puntos y Rectas.Ejercicio 1

Calcula el perímetro del ∆ABC , con A(-1,-2), B(4,2), C(-3,5)
 

Solución:
Sea P= Perímetro

Ejercicio de Áreas *

Pregunta hecha por Anayely en yahoo el 22 de junio del 2010:

En un prado cuadrado de 100 metros de lado, hay cuatro cabras. Cada una atada a una esquina del prado con una cuerda de 50 metros, lo que permite comer una cierta parte de la hierba del prado, quedando en el centro, un trozo que ninguna de ellas alcanza. ¿qué área queda sin pastar?

Cómo un lado del cuadro de la figura mide 100 metros, el área del cuadro es:

10,000 m²

Cómo se puede observar, el área del cuadro que cubre cada cabra con una cuerda de 50 m es la indicada por el círculo de línea punteada. Como se trata de cuatro cabras, tenemos que equivale a un círculo con un radio de 50 m. El área de éste círculo y que corresponde a lo pastado por las cabras, está definida por

A = ¶r²

o sea el área del círculo será igual a

¶ * 2,500 = 7,853. 98163 m²,

restando esta cantidad del área total del cuadro obtenemos el área sin pastar:

10,000 m² - 7,853.98163 m² = 2,146.01837 m²

Ejercicios de ángulos

Calcular el valor de los ángulos internos del hexágono regular inscrito en una circunferencia de 9 centímetros de radio.

Respuesta:

Al tratarse de un hexágono regular no resulta relevante el hecho de estar inscrito en una circunferencia, así como tampoco el tamaño de la misma.

También tengamos en cuenta que la suma de los ángulos internos de cualquier triángulo es igual a 180°.





En este caso se puede observar, que un hexágono regular puede representarse como seis triángulos equiláteros como se muestra.


y estos obviamente, contienen cada uno, 3 ángulos iguales y cada ángulo un valor de 60°



De lo anterior podemos inferir entonces, que cada ángulo interno del hexágono es la suma de dos ángulos de dos triángulos adyacentes como se muestra en la siguiente figura y es igual a 120°.

Finalmente, como el hexágono  cuenta con 6 vértices, el valor de la suma de los ángulos internos es:

Suma de ángulos = 6 x 120° = 720°

El problema de Einstein

Se dice que Albert Einstein es el autor del siguiente problema y también se dice que dijo que el 98% de las personas en el mundo no podrían resolverlo. Investigaré y si encuentro evidencias suficientes les confirmaré la autoria. Por lo pronto y seguramente más interesante pasemos al planteamiento del mismo:

Hechos:

1. Existen 5 casas (sobre una calle) de 5 colores diferentes: azul, verde, rojo, blanco y amarillo.
   
2. En cada casa vive una persona de diferente nacionalidad: británico, danes, alemán, noruego y sueco.
3. Estos 5 dueños toman una cierta bebida: cerveza, café, leche, thé y agua, fuman una cierta marca de cigarrillos: Blue Master, Dunhill, Pall Mall, Prince y Faros, y mantiene una cierta mascota: gato, canario, perro, pez y caballo.
4. Ningún propietario tien la misma mascota, fuma la misma marca de cigarrillos o toma la misma bebida.

Tips:

1. El británico vive en una casa roja.
2. El sueco tiene un perro como mascota.
3. El danés toma thé
4. La casa verde esta a la izquierda de la blanca (junto a ella).
5. El dueño de la casa verde toma café.
6. La persona que fuma Paul Mall cria pájaros.
7. El propietario de la casa amarilla fuma Dunhill.
8. El hombre que vive en la casa que esta en medio toma leche.
9. El noruego vive en la primera casa.
10. El hombre que fuma Faros vive junto al que tiene gatos.
11. El hombre que tiene caballos vive junto al que fuma Dunhill.
12. El propietario que fuma Blue Master toma cerveza.
13. El alemán fuma Prince.
14. El noruego vive junto a la casa azul.
15. El hombre que fuma Faros tiene un vecino que toma agua.

La pregunta es: ¿Quién tiene al pez como mascota?

La próxima semana se publicará la respuesta, esperemos que en ese tiempo ya tengan la solución para compararla.